شانس یا استعداد؛ هرآنچه باید درباره «معناداری آماری» بدانید

جلیل علیزاده، دیجیاتو:

فرض کنید در جمعی نشسته‌اید و فردی ادعا می‌کند که این قدرت را دارد که اگر دو سکه بیندازد هر دو «پشت» بیایند. اگر افراد حاضر در آن جمع با مباحث ابتدایی آمار و احتمال آشنا باشند، احتمالا به این ادعا می‌خندند. چرا که احتمال وقوع دو «پشت» در پرتاب دو سکه چندان غیرممکن نیست.

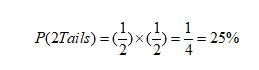
گرچه احتمال وقوع این رویداد کمتر از ۵۰ درصد است، اما احتمال رخداد آن به حدی نیست که افراد متقاعد شوند یک اتفاق ویژه یا به بیان علمی یک «معناداری آماری» رخ داده است. حال فرض کنیم در همان جمع فردی مدعی شود که می‌تواند ۱۰ سکه را به‌ طور پیاپی بیندازد و هر ده سکه «پشت» بیایند. بدیهی است که اگر فرد موفق به انجام ادعای خود شود، افراد حاضر در جمع همگی اذعان خواهند داشت که او استعداد و توانایی ویژه‌ای دارد. اکنون نگاهی به میزان احتمال وقوع این رویداد می‌اندازیم:

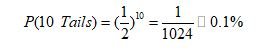
در اینجا شخص مذکور موفق به انجام کاری شده است که احتمال آن ۰.۱ درصد است. بنابراین منطقی به نظر می‌رسد که برای او استعداد و توانایی ویژه‌ای قائل باشیم. اما چه اتفاقی باعث شد که رویداد اولی را یک «معناداری آماری» به حساب نیاوریم اما رخداد دوم را یک «معناداری آماری» به حساب آورده و برای آن فرد استعداد ویژه‌ای قائل باشیم. برای آشنا شدن بیشتر درباره این مفهوم بد نیست نگاهی به تاریخچه آن بیندازیم.

مهمانی سلطنتی، چای انگلیسی و کمی هم آمار و احتمال!

در انگلیس مرسوم است که چای را با شیر مخلوط کرده و می‌نوشند. در یک مهمانی سلطنتی «رونالد فیشر» (Ronald Fisher)، آماردان بریتانیایی یک فنجان چای و شیر به بانویی تعارف می‌کند. زن از فیشر می‌پرسد که آیا ابتدا چای را ریخته و سپس به آن شیر اضافه کرده یا آن که ابتدا شیر ریخته و سپس چای را اضافه کرده است. رونالد فیشر از این سوال جا می‌خورد، چرا که معتقد است وقتی شیر و چای با هم ترکیب شوند (مستقل از آن که کدام یک در ابتدا ریخته شده است)، محصول نهایی طعم و مزه یکسانی خواهد داشت و قابل تشخیص نیست که چه چیزی در ابتدا ریخته شده است.

زن در پاسخ به فیشر می‌گوید که با توجه به اصول خانواده سلطنتی روش صحیح آن است که ابتدا چای ریخته شود و سپس شیر به آن اضافه شود. زن در ادامه ادعا می‌کند که توانایی آن را دارد که پس از چشیدن طعم نوشیدنی نهایی بگوید که آیا ابتدا چای به آن اضافه شده یا شیر؟

رونالد فیشر که یک سوژه جذاب آمار-احتمال پیدا کرده بود (احتمالا جذاب‌تر از یک مهمانی کسل‌کننده)، سریعا به دنبال روشی می‌گردد تا بتواند ادعای زن را صحت‌سنجی کند. او پس از کمی تامل آزمایش زیر را طراحی کرد:

او ۸ فنجان آماده کرد. در ۴ فنجان‌ ابتدا چای و سپس شیر اضافه شد و در ۴ فنجان دیگر ابتدا شیر و سپس چای اضافه شد. همچنین او سعی کرد در این هشت فنجان اصول «آزمایش کنترل شده تصادفی» را رعایت کند و هیچ‌کدام از فنجان‌ها تفاوت چشمگیری از لحاظ دما، میزان شیرین بودن، حجم و… نداشته باشند. سپس او این هشت فنجان را به صورت تصادفی داخل سینی قرار داد و از زن خواست که این هشت فنجان را به ترتیب بچیند. با کمی دانش ترکیبیات می‌توانیم حساب کنیم که این ۸ فنجان می‌توانند ۷۰ چینش مختلف داشته باشند:

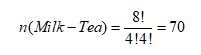
همچنین درنظر داشته باشید تنها ۱ حالت از این ۷۰ حالت مطلوب است. بنابراین احتمال صحیح چیدن این فنجان‌ها حدودا ۱.۴ درصد است.

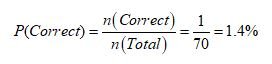
بنابراین اگر بانوی سلطنتی داستان ما بخواهد که به صورت شانسی فنجان‌ها را بچیند، ۷۰ روش احتمالی برای او وجود دارد و تنها یکی از این ۷۰ روش درست است، به عبارت دیگر، تنها ۱.۴ درصد احتمال دارد که او چینش صحیح را قرار دهد.

پس از انجام آزمایش در کمال تعجب رونالد فیشر آن زن توانست فنجان‌ها را دقیقا با چینش درست قرار دهد و باتوجه به اینکه احتمال آن که زن موفق شود به صورت شانسی چینش صحیح را قرار دهد، برای فیشر محرز شد که او استعداد ویژه‌ای در تشخیص فنجان چای و شیر دارد.

این اتفاق سبب شد تا رونالد فیشر به سراغ ایجاد مفهومی به نام «P-Value» یا «مقدار پی» برود که در سال‌های آینده آماردان‌های زیادی به تعمیم و گسترش آن پرداختند. مقدار پی یا P-Value به ما نشان می‌دهد که چه میزان احتمال دارد نتایج بدست آمده صرفا تحت تاثیر شانس یا اتفاق باشد. این موضوع یک ابزار کلیدی در فضای کسب‌وکار و آزمایشگاهی به حساب می‌آید، چرا که ابزار ریاضی نسبتا دقیقی برای صحت‌سنجی فرضیات گوناگون است.

حاشیه خطا و «معناداری آماری»

پس از ایجاد مفهوم «P-Value» این سوال برای اکثر آماردان‌ها پیش آمد که این مقدار p دقیقا چقدر باید باشد. به عبارت بهتر به چه مقداری احتمال کوچک گفته می‌شود؟ رونالد فیشر در ابتدا مقدار ۵ درصد را برای آن پیشنهاد داد که امروزه یک معیار پذیرفته شده است و در اکثر صنایع از آن استفاده می‌شود. به این مقدار حاشیه خطا یا «آلفا» گفته می‌شود که با علامت α نمایش داده می‌شود. به طور مثال اگر حاشیه خطا ۵ درصد باشد، بدین معناست که با احتمال ۹۵ درصد می‌توانیم مطمئن باشیم که نتایج بدست آمده برحسب تصادف یا اتفاق حاصل نشده‌اند.

در بعضی صنایع خاص و مواقعی که دقت بالا موردنیاز است، آزمایشگران حاشیه خطا را ۱ درصد درنظر می‌گیرند. بنابراین اگر حاشیه خطا را یک درصد درنظر بگیریم (که بسیار سخت‌گیرانه است)، با توجه به اینکه P-Value آزمایش شیر و چای رونالد فیشر حدود ۱.۴ درصد بود، در صورتی که زن تمام فنجان‌ها را به صورت صحیح بچیند باز هم نمی‌توان برای او استعداد خاصی قائل شد. لازم به ذکر است که در این شرایط می‌بایست نوع آزمایش را تغییر داد و شرایط آزمایشی را ایجاد کرد که متناسب با حاشیه خطای ذکر شده باشد.

آشنایی با «آزمون فرضیه آماری» و «فرض صفر»

به طور کلی مبحث «معناداری آماری» بر پایه سه اصل استوار است؛

• آزمون فرضیه
• توزیع نرمال
• پی مقدار یا P-Value

فرض کنید که ما ادعایی را مطرح می‌کنیم، که به آن فرض صفر (null hypothesis) می‌گویند. کاری که آزمون فرضیه انجام می‌دهد آن است که با بررسی داده‌ها صحت ادعای اولیه (فرض صفر) را بررسی می‌کند. اگر فرض صفر صحیح نبود، آن گاه به دنبال فرضیه جایگزین می‌گردیم. به منظور بررسی صحت فرض صفر از P-Value کمک می‌گیریم. در صورتی که داده‌ها نشان از صحیح بودن فرضیه جایگزین می‌دادند، آن گاه فرض صفر را رد می‌کنیم و فرضیه جایگزین را می‌پذیریم. به منظور درک بهتر این موضوع بهتر است یک مثال را مطرح کنیم.

سرویس جابجایی اکسپرس

یک سرویس جابجایی مرسوله در شهر مدعی آن است که سفارش هر مشتری را در کمتر از ۳۰ دقیقه به دست او می‌رساند. بنابراین آزمون فرضیه این ادعا به شرح زیر خواهد بود:

• فرض صفر: مدت زمان رسیدن مرسوله به دست مشتری کمتر از ۳۰ دقیقه است.
• فرضیه جایگزین: مدت زمان رسیدن مرسوله به دست مشتری ۳۰ دقیقه یا بیشتر است.

در اینجا هدف از آزمون فرضیه آن است که کدام ادعا (باتوجه به داده‌ها) صحیح‌تر است. برای صحت‌سنجی فرضیه‌ها می‌توان از آزمون Z استفاده کرد تا در نهایت باتوجه به داده‌های بدست آمده یک فرضیه را تایید و دیگری را رد کرد.

آشنایی با توزیع نرمال

توزیع نرمال یا توزیع بهنجار یک تابع چگالی احتمال است که کاربرد زیادی در بسیاری از توزیع‌های داده‌ای دارد.

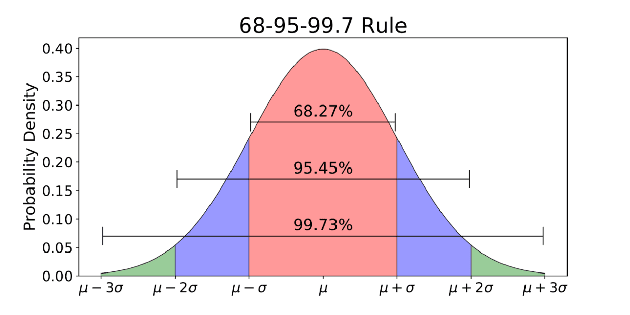
به طور کلی برای این تابع ۳ دسته در نظر گرفته‌ شده (قرمز-بنفش-سبز) که به شرح زیر است؛

• ۶۸ درصد داده‌ها در دسته قرمز قرار دارند.
• ۹۵ درصد داده‌ها در دسته قرمز و بنفش قرار دارند.
• ۹۹.۷ درصد داده‌ها در دسته قرمز، بنفش و سبز قرار دارند.

در اکثر مسائلی که بحث محاسبه پی مقدار یا همان P-Value مطرح می‌شود، مقادیر بدست آمده در قسمت سبز و در مواردی در قسمت بنفش نمودار قرار می‌گیرند. لازم به ذکر است که اگر آزمون فرضیه یک سویه (one-tailed test) داشته باشیم، تنها قسمت سمت راست دسته سبز یا بنفش مقدار «P-Value» ما را نمایش می‌دهد، اما اگر آزمون فرضیه دو سویه (two-tailed test) آنگاه هم قسمت راست و هم قسمت چپ ناحیه سبز و بنفش مقدار «P-Value» را نمایش می‌دهد.

نگاهی دقیق به «پی مقدار» یا «P-Value»

تمام مباحث قبلی که بررسی کردیم، پیش‌زمینه‌ای برای بررسی و فهم دقیق‌تر P-Value بود. همان‌طور که در مباحث قبلی اشاره کردیم، هر آزمون فرضیه از دو بخش «فرض صفر» و «فرضیه جایگزین» تشکیل شده است. پی مقدار قرار است به ما به صورت عددی نشان دهد که آیا واقعه رخ داده براساس شانس و حادثه بوده یا عاملی باعث رخ دادن آن شده است. اگر پی مقدار حاکی از وجود عاملی در رخداد واقعه باشد که به آن همان «معناداری آماری» می‌گوییم، آنگاه فرض صفر را می‌پذیریم. در غیر این صورت فرض صفر  را رد کرده و فرضیه جایگزین را قبول می‌کنیم. هر میزان که پی مقدار کمتر باشد، احتمال آن که رخداد براساس شانس یا حادثه رخ داده باشد، کمتر است.

در مثال فنجان چای و شیر مقدار P-Value حدود ۱.۴ درصد بود، این سخن بدین معناست که تنها ۱.۴ درصد احتمال وجود دارد که این فنجان‌ها به صورت اتفاقی صحیح چیده شده باشند، بنابراین در اینجا فرض صفر را می‌پذیریم و ادعای زن (داشتن استعدادی ویژه) تایید می‌شود. پیش از آن که وارد بحث کاربردهای موضوع پی مقدار در فضای کسب و کار و تصمیم‌گیری داده‌محور شویم، یک مسئله جذاب و کمی چالشی از این مبحث را بررسی خواهیم کرد.

سکه سالم یا خراب

در یک آزمایش آماری، پس از ۲۰ بار پرتاب سکه ۱۴ بار «رو» آمده است. حال می‌خواهیم بررسی کنیم که آیا این سکه سالم (احتمال «رو» یا «پشت» آمدن در آن یکسان باشد) است یا خیر؟ در این مسئله حاشیه خطا یا آلفا را ۵ درصد درنظر می‌گیریم.

در گام اول یک آزمون آماری تعریف می‌کنیم:

• فرض صفر: این سکه سالم است و احتمال «پشت» یا «رو» آمدن در آن یکسان است
• فرضیه جایگزین: این اُریب است و متمایل به «رو» آمدن است.

اکنون باید پی مقدار را محاسبه کنیم. با توجه به فرضیه جایگزین که سکه را اُریب و متمایل به «رو» آمدن می‌داند، P-Value برابر احتمال آن است که در ۲۰ بار پرتاب سکه حداقل ۱۴ بار «رو» بیاید. بنابراین پی مقدار به شکل زیر خواهد بود:

و احتمال حاصل برابر خواهد بود:

لازم به ذکر است که مقدار به دست آمده برای آزمون فرضیه یک سویه است و اگر آزمون فرضیه را دو سویه درنظر بگیریم، یعنی فرضیه جایگزین صرفا آن باشد که سکه اُریب است و از تمایل آن به وجه خاصی سخن نگوییم، مقدار P-Value دو برابر خواهد شد، چرا که باید مشابه همین حالت را برای «پشت» آمدن نیز حساب کنیم.

نتیجه‌گیری

با توجه به اینکه در این مسئله مقدار P-Value بیشتر از ۰.۰۵ است، در حقیقت پی مقدار این مسئله در دسته بنفش تابع نرمال قرار می‌گیرد و اگر بخاطر داشته باشید ۹۵ درصد داده‌ها در دسته قرمز و بنفش قرار داشتند، بنابراین می‌توان گفت که اتفاق عجیبی رخ نداده است و فرض صفر مبنی بر سالم بودن سکه صحیح است.

جالب است بدانید که اگر در پرتاب ۲۰ سکه ۱۵ بار «رو» می‌آمد، پی مقدار برابر ۰.۰۴۱۴ می‌شد و در دسته سبز قرار می‌گرفت و با توجه به اینکه کمتر از ۰.۰۵ می‌شد، آن‌گاه ادعای سالم بودن سکه رد می‌شد و فرضیه اُریب بودن سکه به سمت وجه «رو» تایید می‌شد. بطور کلی استفاده از مفهوم پی مقدار در بحث «معنا‌داری آماری» ابزار فوق‌العاده‌ کارآمدی برای صحت‌سنجی یک ادعا است و استفاده از آن یکی از اصول اولیه «تصمیم‌گیری داده‌محور» است.

تصمیم‌گیری داده‌محور و استفاده از «معناداری آماری» در کسب‌وکار

یکی از مهم‌ترین وظایفی که مدیران محصول و مدیران ارشد در فضای کسب‌وکار با آن روبه‌ رو هستند، تصمیم‌گیری است. این افراد روزانه با ادعاها و فرضیات مختلفی روبه‌رو هستند و باید از صحت و درستی آن‌ها اطمینان یابند تا بتوانند بهترین تصمیم را اتخاذ کنند. بدیهی است که مجموعه‌ای از تصمیم‌ها و استراتژی‌های غلط توسط مدیران محصول و ارشد به تدریج باعث شکست و در نهایت از بین رفتن سازمان خواهد شد. بنابراین در اینجا بحثی به نام «تصمیم‌گیری داده‌محور» مطرح می‌شود تا خطای تصمیم‌گیری مدیران را به حداقل برساند.

یکی از متداول‌ترین روش‌ها برای صحت‌سنجی و ارزیابی ادعاها استفاده از «آزمون فرضیه آماری» است. به طور مثال ادعای زیر را می‌توان با «آزمون فرضیه آماری» صحت‌سنجی کرد:

• مدیر یک فروشگاه آنلاین ادعا می‌کند که با ارائه تخفیف‌های بیشتر می‌تواند ارزش طول عمر مشتریان (CLV) را افزایش دهد.
• یک باشگاه ورزشی در حال بستن قرارداد با یک تولیدی لباس است. این تولیدی لباس مدعی آن است که تنها ۲ درصد از تولیدات آن‌ها دچار نقص و ایراد است.
• یک شرکت سرمایه‌گذاری به شما پیشنهاد می‌کند که به جای سرمایه‌گذاری در بازار فارکس در بازار رمزارزها سرمایه‌گذاری کنید، چرا که در سه سال گذشته بازدهی بیشتری داشته است.
• مدیر مارکتینگ یک شرکت پوشاک باور دارد که سویشرت‌ و هودی‌های شرکت بین مردان ۱۵ تا ۳۰ سال طرفداران بیشتری دارد، بنابراین باید یک کمپین تبلیغاتی اختصاصی برای جذب این رده سنی انجام داد.
• مشاور مدیریت یک شرکت نرم‌افزاری توصیه می‌کند که توسعه‌دهندگان کم‌تجربه و مبتدی شرکت در دوره‌های مجزا آموزشی شرکت کنند تا در مدت زمان کمتری بتوانند باتجربه و ارشد شوند.

هر یک از ادعاهای ذکر شده را می‌توان با جمع‌آوری داده‌های مناسب و انجام آزمون فرضیه آماری صحت‌سنجی کرد. ایجاد فرهنگ «تصمیم‌گیری داده‌محور» در یک سازمان علاوه‌بر اینکه باعث افزایش بازدهی و بهبود عملکرد تک تک بخش‌های مجموعه می‌شود، در طولانی مدت فرهنگ شرکت را نیز دگرگون خواهد کرد و افراد شرکت به صورت ناخودآگاه به دنبال داده و شواهد برای ادعاهای خود خواهند گشت و از بیان ادعاها شهودی و تصمیم‌گیری احساسی پرهیز خواهند کرد.